О некоторый возможностях современного квантово-механического ПО
Известно, что прогресс в вычислительной технике в период последних 5-ти лет позволил выйти квантово-механическому моделированию из суперкомпьютерных центров к «широкому кругу» пользователей путем повсеместного внедрения
в университетах и на производстве недорогих, но высокопроизводительных
вычислительных кластеров. Квантово-механическое ПО развивается не менее
быстрым темпом.
Рассмотрим некоторый возможности современного ПО для проведения квантово-механических расчетов при моделировании наноструктур.
Наиболее качественные результаты моделирования возможны при использовании ПО, реализующего методы теории функционала плотности
(ТФП), или ab-initio методы (моделирование «из первых принципов»).
Результаты моделирования, приведенные в этой статье получены на условно-бесплатном ПО, использующем ТФП (англ. DFT): AbInit, Siesta, Dacapo, Exciting, Fleur, Elk, FHImd.
Молекулярная динамика наноструктур. Молекулярная
динамика – подход, при котором моделируют движение каждого атома в
молекулярной системе для того, чтобы наблюдать кинетическое поведение
системы и ее свойства в равновесном состоянии при заданных параметрах
окружающей среды.
 Кристалл меди при Т=0 К Кристалл меди при Т=0 К
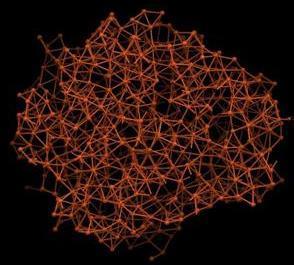 Кристалл меди (распад) при Т=2000 К Кристалл меди (распад) при Т=2000 К
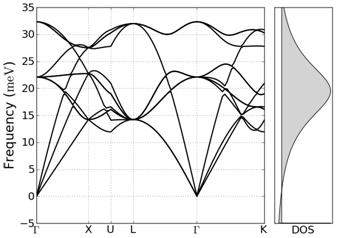 Фононный спектр кристалла меди Фононный спектр кристалла меди
Прочностные расчеты наноструктур путем построения энергетических зависимостей для последующего определения модуля упругости.
Предлагается добиться упрочнения покрытий из нитрида и карбида титана введением примесей порядка 1–2 % .
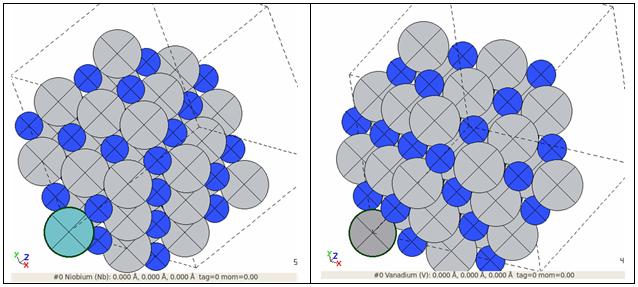 Введение атома примеси ниобия (слева) и ванадия (справа) в супер-ячейку массива нитрида титана Введение атома примеси ниобия (слева) и ванадия (справа) в супер-ячейку массива нитрида титана
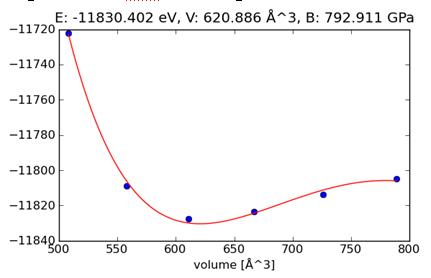 Построение энергетической зависимости супер-ячейки объемного нитрида
титана от ее размера, для нахождения модуля упругости по методу
Бирч-Мурнагана, примесь Nb, модуль упругости B = 793.
Построение энергетической зависимости супер-ячейки объемного нитрида
титана от ее размера, для нахождения модуля упругости по методу
Бирч-Мурнагана, примесь Nb, модуль упругости B = 793.
Упрочнение примесями переходных металлов показало достаточно высокую
эффективность, в особенности танталом Ta (прочность возросла на 29% для
TiN и на 42% для TiC) и ниобием Nb (прочность возросла на 28% для TiN и
на 41% для TiC).
Определение устойчивых конфигураций интерметаллидов путем построения фазовых диаграмм. Графическим способом описания фаз, находящихся в состоянии равновесия, является диаграмма состояния.
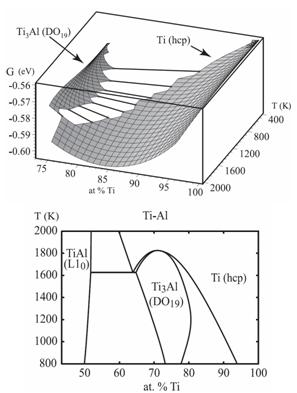 Фазовые диаграммы для интерметаллида TiAl в 3D и 2D Фазовые диаграммы для интерметаллида TiAl в 3D и 2D
Получено пространство состояний интерметаллидов семейства TiAl,
широко применяемых в качестве упрочняющих покрытий. Выявлены устойчивые
состояния конфигураций интерметаллидов на диапазоне температур и
концентраций путем расчета и построения фазовых диаграмм и распределений
энергии.
Расчет распределения электронной плотности (англ. DOS) и зонной структуры (англ. BAND) вещества.
Расчет распределения электронной плотности и зонной структуры
необходим для исследования электродинамических свойств материалов.
Расчеты разрешенных и запрещенных зон, значений электронной плотности на
уровне Ферми используются для анализа электронных свойств в основном
для полупроводниковых материалов и диэлектриков, изучения явления
сверхпроводимости.
Исследование взаимодействий материалов на границе сред.
Прочность сцепления материалов между собой (подложки и покрытия)
определяется величиной энергетического барьера перемещения атома
покрытия из текущей ячейки, состоящую из атомов подложки, в соседнюю
ячейку кристаллической решетки.
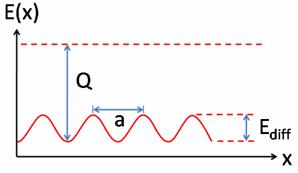 Энергетический ландшафт поверхности наноструктуры при диффузии на ней
атомов в одном измерении (Х – ось перемещения атомов по поверхности
подложки), Q-энергия связи взаимодействий на границе сред, Ediff
является барьером для диффузии, a – расстояние между соседними узлами
адсорбции
Энергетический ландшафт поверхности наноструктуры при диффузии на ней
атомов в одном измерении (Х – ось перемещения атомов по поверхности
подложки), Q-энергия связи взаимодействий на границе сред, Ediff
является барьером для диффузии, a – расстояние между соседними узлами
адсорбции
Миграция материала покрытия (титан, в данном исследовании) не
является свободной вследствие наличия энергетических барьеров, которые
имеются на поверхности подложки с правильной кристаллической решеткой
(гексагональной в случае кобальта, в данном исследовании). При диффузии
(адсорбции) на границе кристаллов возникает энергетическая
неоднородность вследствие периодичности в расположении элементов
кристаллической решетки, которая препятствует этим процессам
пропорционально энергетическому барьеру, который можно рассчитать,
используя методы квантово-механической оптимизации (применяется метод
«QuasiNewton»).
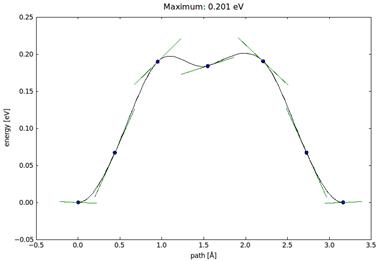 Энергетический барьер (Ediff=0.201 eV) для атома титана на поверхности кобальта Энергетический барьер (Ediff=0.201 eV) для атома титана на поверхности кобальта
По величине энергетического барьера (Ebarr= 0.201 eV для преодоления
расстояния около 3A) следует судить о прочности позиционирования
покрытия на подложке. При условии достаточно высокого барьера какая-либо
динамика на границе материалов затруднительна, в том числе при внешних
механических и температурных воздействиях.
Продолжение следует…
- Источник(и):
ФГБОУ ВПО Комсомольский-на-Амуре государственный технический университет - http://www.nanonewsnet.ru/articles/2012/o-nekotoryi-vozmozhnostyakh-sovremennogo-kvantovo-mekhanicheskogo-po
|