Физики сымитировали нарушение неравенств Белла в «классическом» эксперименте

Международная научная группа, в которую вошли сотрудники Национального университета Сингапура и Норвежского технологического университета, показала, как в «классическом» эксперименте можно сымитировать нарушение неравенств Белла.

Неравенства Белла, напомним, формулируются как универсальные статистические критерии, применимые в опытах с двумя частицами, которые взаимодействовали друг с другом, а затем оказались разделены. Выполняя какие-либо измерения (обычно измеряемым параметром становится направление вектора поляризации фотонов) над каждой частицей из множества пар, наблюдатели фиксируют статистику результатов. После этого собранные данные подставляют в неравенство; если оно не выполняется, следует вывод о том, что изученная система имеет квантовую природу.

Полученные результаты становятся абсолютно надёжными только тогда, когда экспериментаторы дают полное описание приборов и методики измерений (несложно представить себе, что нужную статистику могут создавать не два реальных и независимых измерительных устройства, а, скажем, компьютерные программы) и закрывают все «лазейки».

Пример опыта с незакрытыми «лазейками», в котором один фотон из пары частиц перед измерением направлялся на оптический усилитель, мы рассматривали весной. Изменяя настройки оборудования, авторы той работы могли продемонстрировать и выполнение неравенства, и его нарушение.

Основой своего опыта учёные из Сингапура и Норвегии сделали совершенно стандартную схему Клаузера — Хорна — Шимони — Хольта. Запутанные по поляризации пары фотонов создавались путём спонтанного параметрического рассеяния — процесса, который можно представить себе как распад фотонов когерентного лазерного излучения, поступающих в нелинейную среду, на пары частиц с суммарными энергией и импульсом, равными энергии и импульсу исходного кванта света. Одна из частиц направлялась к первому легитимному наблюдателю (Алисе), другая — ко второму (Бобу). И Алиса, и Боб измеряли поляризацию в двух возможных базисах, случайным образом выбирая один из них с помощью светоделительного элемента, на обоих выходах которого стоял поляризатор, оснащённый парой однофотонных детекторов на лавинных фотодиодах (ЛФД).

В такой схеме обрабатываются только случаи одновременной регистрации фотонов Алисой и Бобом (если один из квантов света «теряется», событие отбрасывается). По результатам измерений физики определяют параметр Е, в котором учитываются вероятности Р всех возможных исходов одновременной регистрации, и вычисляют коэффициент S. Формулы для расчёта Е и S приведены на рисунке ниже; обозначения А, А’ и В, В’ соответствуют измерениям на стороне Алисы и Боба.

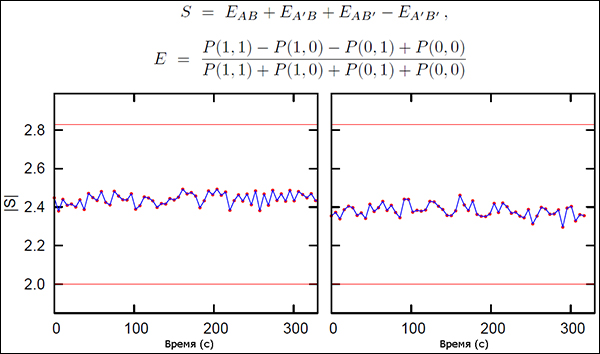Рис. 1. Формулы для вычисления Е и S и результаты расчёта для эксперимента, выполненного без нелегитимного наблюдателя (слева) и в схеме с Евой (иллюстрация из журнала Physical Review Letters).

Само неравенство Клаузера — Хорна — Шимони — Хольта, одна из форм неравенств Белла, выглядит так:

|S| ≤ 2.

Если оно не выполняется, можно утверждать, что в эксперименте наблюдались запутанные состояния фотонов. Математический предел значения |S| равен, как несложно догадаться, четырём, но действительные квантовомеханические состояния обеспечивают только |S| < 21,5.

Упомянутое устройство манипулирует сигналами на выходе лавинных фотодиодов. Напомним, что в нормальном режиме работы попадание фотона на ЛФД приводит к образованию электронно-дырочной пары, которая разделяется приложенным напряжением и создаёт лавину, выдавая макроскопический ток; когда последний превышает некое пороговое значение, приход кванта света регистрируется. Лавинный ток при этом подпитывается зарядом, хранимым небольшой ёмкостью, и схеме, обнаружившей одиночный фотон, требуется некоторое время на восстановление. Если на фотодиод подавать такой поток излучения, что полная перезарядка в коротких промежутках между отдельными фотонами будет невозможна, амплитуда импульса от одиночных квантов света может оказаться ниже порога срабатывания, и детектор «ослепнет». Дальнейшее повышение оптической мощности позволяет довести количество рождающихся электронно-дырочных пар до того значения, при котором ток превысит пороговое значение без возбуждения лавины.

Выбирая нужную поляризацию и мощность оптических импульсов, отсылаемых Бобу, Ева может инициировать сигнал на выходе любого из четырёх ЛФД, доступных легитимному наблюдателю. Боб, таким образом, будет регистрировать «классические» световые импульсы, а результаты его измерений будут контролироваться Евой.

В эксперименте с Алисой, Евой и Бобом физики получили коэффициент S = 2,381 ± 0,036. При таком значении неравенство Клаузера — Хорна — Шимони — Хольта, очевидно, нарушается, что свидетельствует о потенциальной уязвимости протокола квантового распределения ключей (Е91). В этом протоколе, предложенном в 1991 году Артуром Экертом, используются запутанные пары фотонов, а проверка неравенств Белла считается средством обнаружения Евы.

Поскольку авторы, управляя действиями Евы, могли сфабриковать любой результат, никакой необходимости сохранять источник запутанных фотонов не было. В отдельном опыте источник заменили парой таких устройств, какими располагал нелегитимный наблюдатель, и неравенство вновь оказалось нарушено.

Выступление на недавней конференции QCRYPT 2011 одного из участников нового исследования Вадима Макарова, посвящённое уязвимостям систем квантового распределения ключей:

Полная версия отчёта опубликована в журнале Physical Review Letters.

Источник(и):

1. Nature News

2. compulenta.ru

http://www.nanonewsnet.ru/articles/2011/fiziki-symitirovali-narushenie-neravenstv-bella-v-klassicheskom-eksperimente